Solving sudokus with BrainScaleS-2
In this task we want to apply our newly gained knowledge to a well-known problem: We will deal with solving a sudoku on spiking hardware.
If you never before encountered this logic puzzle from 1984, let’s define the rules. Usually you have a 9x9 square grid and the goal is to fill in numbers from 1 to 9, given crucial constraints:
In each row, each number is only allowed exactly once.
In each column, each number is only allowed exactly once.
In each 3x3 sub grid, each number is only allowed exactly once.
To find a valid solution, hints are given in form of given, fixed numbers. An obvious strategy for solving a sudoku is to, sequentially, find a square where only one number is allowed. This seems trivial but due to the high dimensionality finding a solution is a non-trivial task. However, checking the correctness of a potential solution is a simple task. To circumvent the slowness of a brute-force solution one can resort to a stochastic strategy. In fact, a spiking neuronal network (SNN) can accomplish this task in this manner quickly and with high precision.
The basic idea in creating a sudoku solver with an SNN is to assign to each possible number in each field one neuron, called one-hot encoding. In our case, each field would have four neurons representing the numbers 1 to 4, respectively. A neuron being active is interpreted as that field being filled with the respective number, consequently a given, hinted number is represented by a continuously spiking neuron. An excluding constraint will be realised with an inhibitory synapse due to the suppressing effect on the activity. To allow the network to explore different states, a random Poisson-distributed background noise is applied to all neurons. In addition, each neuron is excitatorily connected to itself to maintain possible activity.
Let’s start with a simplified version of a sudoku with a 4x4 grid, as shown in the figure. Assume the grey three is given, applying the previously mentioned constraints we obtain:
Due to 1, the purple threes are not allowed.
Due to 2, the green threes are not allowed.
Due to 3, the blue threes are not allowed.
Due to the choice of our encoding, the orange numbers are not allowed (in each field only one number is allowed to be active)
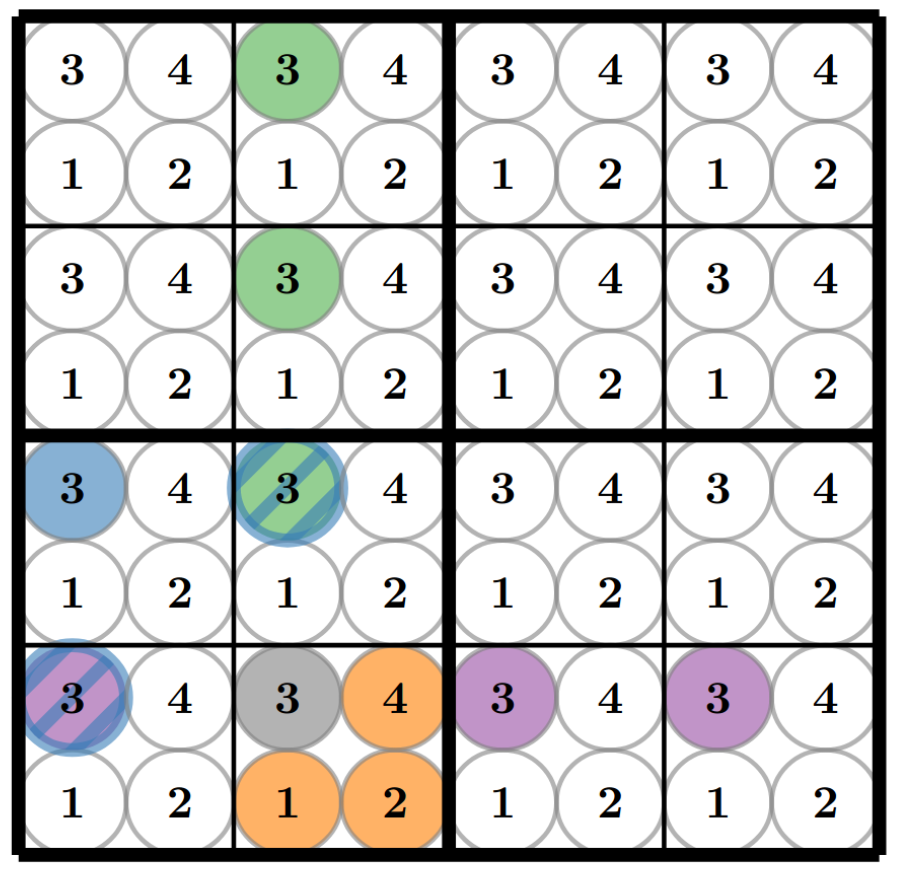
Representation of a 4x4 sudoku with one-hot encoding: In each small square, each number from 1 to 4 has one respective neuron; four small squares, framed by the thick line, make one block in the original sudoku; there are four such blocks to complete the 4x4 sudoku.
For further information read into Solving the Constraint Satisfaction Problem Sudoku on Neuromorphic Hardware (MA Thesis).
Experiment setup
We start by creating a population with the required number of neurons. Additionally, we create a view for each field to facilitate easier access later
pops_collector[row][field][neuron]
# Defining total runtime and dimensionality of sudoku
runtime = 0.5
dimension = 4
# -> we need 4 (rows) * 4 (columns) * 4 (numbers) = 4^3 neurons
pop = pynn.Population(dimension**3, HXNeuron())
pop.record("spikes")
# to define the connections easier, we save a "view" of each neuron in a list
pops_collector = []
for row in range(dimension):
pops_row = []
for field_in_row in range(dimension):
pops_field = []
for number_in_field in range(dimension):
neuron = pynn.PopulationView(
pop,
[row * dimension**2 + field_in_row * dimension
+ number_in_field])
pops_field.append(neuron)
pops_row.append(pops_field)
pops_collector.append(pops_row)
# Create background noise
poisson_source = pynn.Population(dimension**3,
SpikeSourcePoisson(duration=runtime - 0.01, rate=5e5, start=0.01))
# connect random sources with neurons
# additionally each neuron is connected to itself excitatorily to
# sustain possible activity
pynn.Projection(pop,
pop,
pynn.OneToOneConnector(),
synapse_type=StaticSynapse(weight=20),
receptor_type='excitatory')
pynn.Projection(poisson_source,
pop,
pynn.OneToOneConnector(),
synapse_type=StaticSynapse(weight=30),
receptor_type='excitatory')
# create stimulation for clues and connect to according neurons
stim_given_numbers = pynn.Population(
1, SpikeSourceArray(spike_times=np.linspace(0.0, runtime, 500)))
clue_projections = []
for row in range(4):
clues_row = []
for column in range(4):
clues_field = []
for number in range(4):
clues_field.append(pynn.Projection(
stim_given_numbers,
pops_collector[row][column][number],
pynn.AllToAllConnector(),
synapse_type=StaticSynapse(weight=0),
receptor_type='excitatory'))
clues_row.append(clues_field)
clue_projections.append(clues_row)
# functions to solve the sudoku:
def set_clues(clues=None):
"""Sets the clues in the network."""
if clues is None:
clues = np.zeros((4, 4), dtype=int)
for row, row_clues in enumerate(clue_projections):
for col, field_clues in enumerate(row_clues):
for number, clue_projection in enumerate(field_clues, start=1):
for connection in clue_projection:
connection.weight = 63. if clues[row,col] == number else 0.
def hide_solution(grid, num_clues, seed=None):
"""Hides the solution and only leaves `num_clues` hints."""
indices = np.argwhere(np.logical_and(grid > 0, grid <= 4))
if len(indices) < num_clues:
raise RuntimeError(
f"The sudoku has less than {num_clues} clues, which is the number of required clues :(")
np.random.seed(seed)
indices = indices[np.random.choice(len(indices), num_clues, replace=False)]
clues = np.zeros_like(grid)
clues[(indices.T[0], indices.T[1])] = grid[(indices.T[0], indices.T[1])]
return clues
def get_solution(runtime, clues):
"""Executes the network and returns the current solution."""
set_clues(clues)
grid = np.zeros((4, 4), dtype=int)
# Define duration of poisson spikes
poisson_source.set(duration=runtime - 0.01)
# emulate the network
pynn.reset()
pynn.run(runtime)
# read back solution
for row, row_populations in enumerate(pops_collector):
for col, field_populations in enumerate(row_populations):
num_spikes = [
len(num_population.get_data("spikes").segments[-1].spiketrains[0])
for num_population in field_populations
]
grid[row, col] = np.argmax(num_spikes) + 1
return grid
# Constraints
# create inhibitory connections to neurons in the same field
# representing different numbers
# create inhibitory connections to neurons in the same row
# representing the same number
# create inhibitory connections to neurons in the same column
# representing the same number
# create inhibitory connections to neurons in the same block
# representing the same number
from functools import partial
from collections import OrderedDict
from ipywidgets import interactive, IntSlider, FloatSlider, Layout,\
VBox, Box, HTML
layout = {"width": "calc(100% - 10px)"}
style = {"description_width": "120px"}
IntSlider = partial(IntSlider, continuous_update=False)
controls_parameter = OrderedDict([
("num_clues", ("Number Hints", (0, 16), 8, "config")),
("random_seed", ("Random Seed", (0, 65636), 1234, "config")),
("runtime", ("Runtime", (.1, 10), .5, "config"))
])
headers = {
"config": "Configuration",
}
def build_gui(callback,
controls,
config=None,
defaults=None,
copy_configuration=False):
"""
Build a slider-based GUI for an experiment callback function.
The sliders are grouped by the specific circuit they affect and the
callback's result (e.g. graph) is displayed above the sliders.
"""
print(config)
if config is None:
config = {}
if defaults is None:
defaults = {}
# instantiate sliders according to list of parameters provided by the user
sliders = OrderedDict()
for con in controls:
spec = controls_parameter[con]
default = defaults[con] if con in defaults else spec[2]
if copy_configuration and con in last_configuration:
default = last_configuration[con]
if con != "runtime":
sliders[con] = IntSlider(min=spec[1][0],
max=spec[1][1],
step=1,
value=default,
description=spec[0],
layout=layout,
style=style)
else:
sliders[con] = FloatSlider(min=spec[1][0],
max=spec[1][1],
step=.1,
value=default,
description=spec[0],
layout=layout,
style=style)
widget = interactive(callback, **sliders, **config)
# group sliders according to their sections
sections = OrderedDict()
for con, slider in sliders.items():
header = controls_parameter[con][3]
if header not in sections:
sections[header] = OrderedDict()
sections[header][con] = slider
# build UI according to hierarchical structure from above
u_i = []
for header, children in sections.items():
u_i.append([])
u_i[-1].append(HTML(f"<h3>{headers[header]}</h3>"))
for slider in children.values():
u_i[-1].append(slider)
output = widget.children[-1]
# define custom layout following the responsive web design paradigm
slider_box = Box(tuple(VBox(tuple(s)) for s in u_i), layout=Layout(
display='grid',
grid_template_columns='repeat(auto-fit, minmax(400px, 1fr))',
width='100%'
))
display(VBox([slider_box, output]))
widget.update()
import pynn_brainscales.brainscales2 as pynn
from typing import Callable
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
class SudokuPlotter():
def __init__(
self,
dimension: int,
pop: pynn.populations.Population,
set_clues: Callable[[np.ndarray], None],
hide_solution: Callable[[np.ndarray, int, int], np.ndarray],
get_solution: Callable[[float, np.ndarray], np.ndarray]
):
# Initialize and contain sudoku solver and plotter
"""
Initialize a Sudoku Plotter
:param dimension : Size of Sudoku to solve
:param pop : pynn.Population of Neurons which run emulation
:param set_clues(clues:np.ndarray) : function which sets clues
on population
:param hide_solution(sudoku, num_clues, seed=None) : Chooses random
hints from sudoku returns clues
:param get_solution(runtime: float, clues:np.ndarray) : Runs pynn and
return solved sudoku
"""
self.dimension = dimension
self.pop = pop
# Sudoku Params
self.clues = None
self.solved_sudoku = np.zeros((dimension, dimension))
self.solved_sudoku_correct = None
# Required functions to solve sudoku
self.set_clues = set_clues
self.hide_solution = hide_solution
self.get_solution = get_solution
# Config grid itself
self.grid_color = "gray"
self.grid_width = 2
self.grid_major = 4
# Config numbers on grid
self.sudoku_fontsize = 15
# Config Activities
self.space_between_numbers = 2
self.space_between_cells = 4
self.runtime = None
def empty_sudoku(self, ax: plt.axes) -> None:
"""
Draws onto an axis an empty sudoku grid with dimensions of
self.dimension
param: ax: plt.axis : Axis to draw on sudoku
"""
# Draw outer box
outer_box = [[.5, self.dimension + .5, self.dimension + .5, .5, .5],
[.5, .5, self.dimension + .5, self.dimension + .5, .5]]
# Coloring outer edge
color_outer = self.grid_color
if self.solved_sudoku_correct:
color_outer = "green"
if not self.solved_sudoku_correct:
color_outer = "red"
ax.plot(outer_box[0], outer_box[1], linewidth=8, zorder=20,
color=color_outer)
ax.set_xlim(min(outer_box[0]) * 0.85, max(outer_box[0]) * 1.0125)
ax.set_ylim(min(outer_box[1]) * 0.85, max(outer_box[1]) * 1.0125)
# Arange fine lines for squares
grid_lines = np.arange(.5, self.dimension + .5, 1)
# Draw squares on grid
ax.vlines(grid_lines, min(outer_box[0]), max(outer_box[0]),
linewidth=self.grid_width, color=self.grid_color)
ax.hlines(grid_lines, min(outer_box[0]), max(outer_box[0]),
linewidth=self.grid_width, color=self.grid_color)
# If a propper sudoku draw thick lines onto grid
if self.dimension in [2, 4, 9, 16, 25, 36, 49]:
step = int(np.sqrt(self.dimension))
ax.vlines(grid_lines[::step], min(outer_box[0]), max(outer_box[0]),
linewidth=self.grid_major, color=self.grid_color)
ax.hlines(grid_lines[::step], min(outer_box[0]), max(outer_box[0]),
linewidth=self.grid_major, color=self.grid_color)
# Align ticks as neurons are labeled
ax.set_xticks(np.arange(1, self.dimension + 1, 1))
ax.set_yticks(np.arange(1, self.dimension + 1, 1),
np.arange(self.dimension, 0, -1))
ax.grid(False)
def sudoku_populate(
self, ax: plt.axes, sudoku: np.ndarray
) -> None:
"""
Insert Numbers from a given sudoku. If field equal 0 no number
is written
:param ax: plt.axes : Insert numbers onto this axes.
Run before self.empty_sudoku() to create grid
:param sudoku: numpy.ndarray : Sudoku with 0 for empty cells
"""
for y_coord, values in enumerate(sudoku):
y_coord = len(values) - y_coord
for x_coord, value in enumerate(values):
x_coord = x_coord + 1
if value != 0:
ax.text(x_coord, y_coord, value,
ha="center", va="center",
fontsize=self.sudoku_fontsize)
def sudoku_populate_clues(self, ax: plt.axes,
sudoku: np.ndarray) -> None:
for y_coord, values in enumerate(sudoku):
y_coord = len(values) - y_coord
for x_coord, value in enumerate(values):
x_coord = x_coord + 1
if value != 0:
ax.add_patch(Rectangle((x_coord - .5, y_coord - .5), 1, 1,
fc=(.85, .85, .85), zorder=-11))
def check_solution(self, sudoku) -> bool:
"""
Checks if a sudoku is correct by checking sum in each row.
Expected value is
x_exp = 1 + ... + dimension
:param sudoku:np.ndarray
return bool
"""
expected_result = np.sum(np.arange(1, self.dimension + 1))
for row in sudoku:
if expected_result != np.sum(row):
return False
return True
def solve_sudoku(self, sudoku, runtime, num_clues, seed=None) -> None:
"""
Executes required steps to solve sudoku
1. Defines clues -> SudokuPlotter.clues
2. Applies clues with set_clues
3. Runs emulation (get_solution) and stores in
SudokuPlotter.solved_sudoku
4. Checks if solution correct with SudokuPlotter.ckeck_solution
"""
# Generate clues
self.clues = self.hide_solution(sudoku, num_clues, seed=seed)
self.set_clues(self.clues)
# Solve sudoku
self.solved_sudoku = self.get_solution(runtime, self.clues)
self.solved_sudoku_correct = self.check_solution(self.solved_sudoku)
self.runtime = runtime
def plot_sudoku(self, ax=None, figsize=(4, 4)) -> None:
"""
Plots sudoku
If no axis is given, a new figure is created
"""
if ax is None:
_, ax = plt.subplots(figsize=figsize)
self.empty_sudoku(ax)
self.sudoku_populate(ax, self.solved_sudoku)
self.sudoku_populate_clues(ax, self.clues)
def plot_activities(self, ax=None, figsize=(15, 10)) -> None:
"""
Plots the activity of each individual neuron
If no axis is given, a new figure is created
"""
if ax is None:
_, ax = plt.subplots(figsize=figsize)
spiketrains = self.pop.get_data().segments[-1].spiketrains
colors = plt.get_cmap("tab10").colors[:self.dimension]
# Running vaiable for spacing
current_y = 0
for index, spikes in enumerate(spiketrains):
# Action between different cells
if index % self.dimension == 0 and index > 0:
# Draw a horizontal line to split cells
ax.axhline(current_y + self.space_between_cells / 2,
color="k", alpha=.5)
current_y += self.space_between_cells
# Only add labels in first cell
label = index % self.dimension + 1 if index < self.dimension \
else None
# Plot the acitvity
ax.scatter(spikes, [current_y] * len(spikes), label=label,
color=colors[index % self.dimension], s=10)
current_y += self.space_between_numbers
print(f"xlim Values: {ax.get_xlim()}")
ax.set_xlim(ax.get_xlim()[0], self.runtime * 1.08)
ax.legend()
# Set y labels at center of cells
first_label = self.dimension * self.space_between_numbers / 2
space_between_labels = self.dimension * self.space_between_numbers + \
self.space_between_cells
ticks = np.arange(self.dimension**2) * space_between_labels + \
first_label
numbers = np.arange(self.dimension) + 1
labels = [f'[{row},{column}]'
for row, column in product(numbers, numbers)]
ax.set_yticks(ticks)
ax.set_yticklabels(labels)
ax.set_xlabel("Time [ms]")
ax.set_ylabel("Coordinat [row, column]")
def plot(self, grid=True, figsize=(15, 5)) -> None:
"""
Plots the results
if grid is True, makes one plot with grid and anctivities, else two
separate images
:param grid=True: plots a grid
:param figsize=(15,5): standart size of figure, suggested to have a
ratio 3:1
"""
# self.solve_sudoku(sudoku, runtime, num_clues, seed=seed)
if grid:
fig = plt.figure(figsize=figsize)
grid = GridSpec(3, 8, figure=fig, wspace=1.5)
ax1 = fig.add_subplot(grid[:, :3])
self.plot_sudoku(ax=ax1)
ax2 = fig.add_subplot(grid[:, 3:])
self.plot_activities(ax=ax2)
else:
self.plot_sudoku()
self.plot_activities()
SP: SudokuPlotter = SudokuPlotter(dimension, pop, set_clues, hide_solution, get_solution)
# this sudoku shall be solved
global sudoku
sudoku = np.array([
[3, 2, 4, 1],
[1, 4, 3, 2],
[2, 3, 1, 4],
[4, 1, 2, 3]
])
# The cell below will only work, of course, if you implemented the correct constraints above.
# Red/green frame show (in)correctness of the proposed solution (consistency with the given sudoku).
def experiment(**kwargs):
SP.solve_sudoku(sudoku, kwargs["runtime"], kwargs["num_clues"], kwargs["random_seed"])
SP.plot()
# plt.savefig("solved_sudoku.png", backend="png", bbox_inches="tight")
build_gui(experiment, ["num_clues", "random_seed", "runtime"])
The hardware will try to solve the given sudoku. If you want to implement your own sudoku with unknown numbers you can enter 0 as an empty field. (Hint: When you change the sudoku, rerun the cell)
The hints are chosen randomly. By varying the seed you vary the position of the clue and by changing the number the sudoku changes the difficulty.
Exercises
Task 1: Run the network without any constrains, observe the spike pattern and the solution of the sudoku. Try to explain.
Task 2: Now implement the four constraint rules discussed above. If they are correctly implemented you should get a solved sudoku (keep number of hints and seed).
Now you have a working sudoku solver. Let’s test it:
Task 3: Vary the number of clues. If the solver fails can you find an explanation for that behavior? Can you think of possible strategies to reduce such errors? (It might help to inspect the code and numpy documentation)
Task 4: What do you expect to happen, if you set the number of clues to zero? Check your hypothesis. Can you explain your observation?
Task 5: Now, investigate how the success rate is related to the number of clues. For this, vary the number of clues from four to ten. Repeat each configuration ten times, while keeping the sudoku fixed. Visualize your result.
Task 6: Is there a constraint that is not necessarily required? Why?
Task 7: Crunching some numbers: How many neurons and how many synaptic connections were required in this task? How many would be required for a 9x9 sudoku?